In his work Synergetics (1997), R. Buckminster Fuller introduced another tetrahedral shape, known as the T-Quanta Module. Like the A & B Quantum Modules, the T-Quantum springs from numerous well-known polyhedral geometries. For instance, consider the Rhombic Triacontahedron.
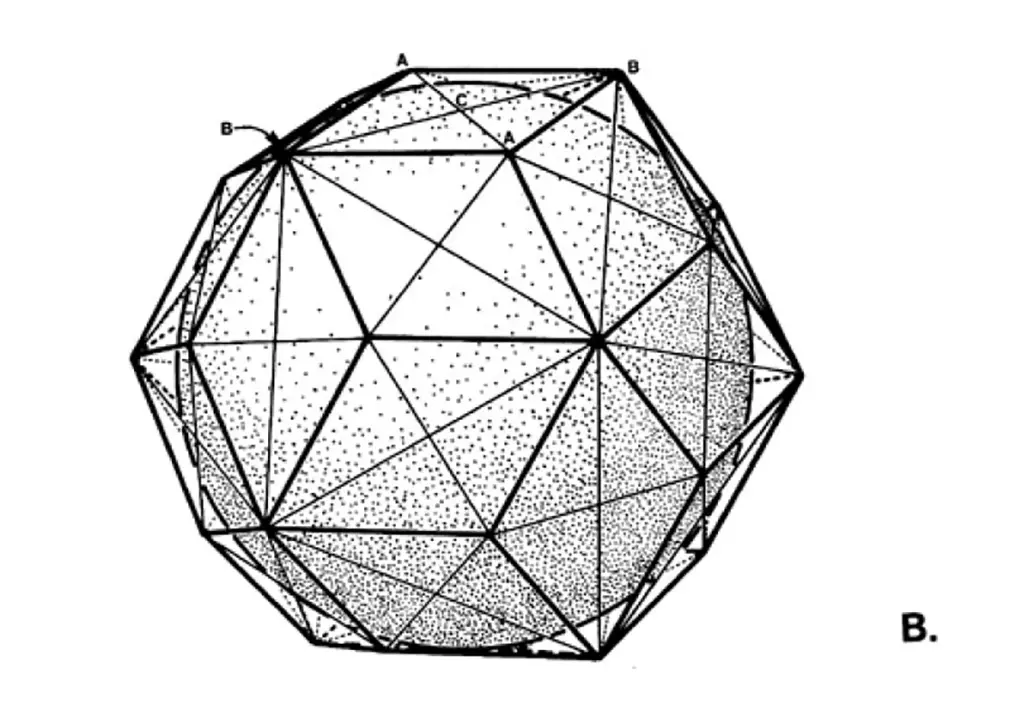
Fig. 986.405 B – Division of a face of the Rhombic Triacontahedron into four triangles
Firstly, we divide one of its faces into four right-angled triangles by joining opposite vertices. Then, we draw lines from the corners of this triangle to the center of the Rhombic Triacontahedron. This action forms an irregular tetrahedron that we identify as the T Quanta Module.
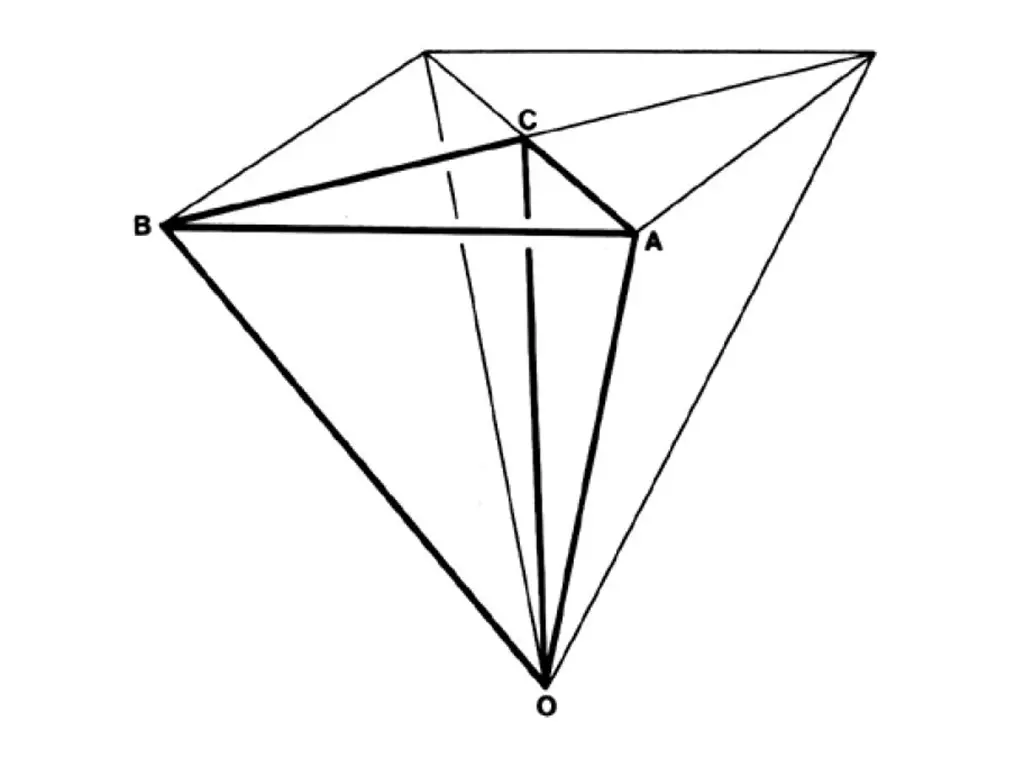
Fig. 986.411C – T Quanta Module derived from the Rhombic Triacontahedron
Since the Rhombic Triacontahedron features 30 congruent Faces, we can depict it as an assembly of 120 T Quanta Modules. Of these, half represent mirrored versions, referred to as positive and negative by Fuller himself.
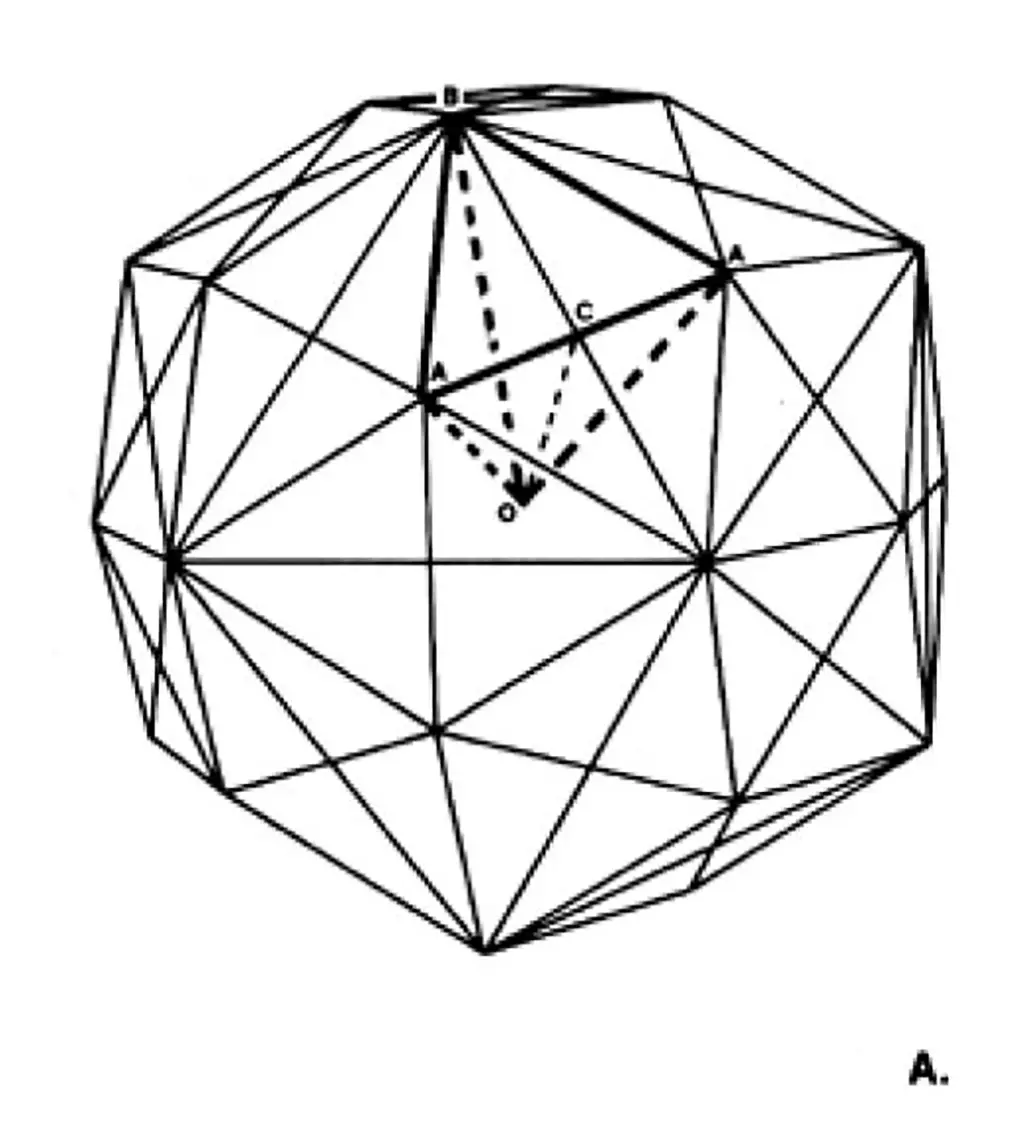
Fig. 986.419 A – T Quanta Modules within the Rhombic Triacontahedron
This method’s vertices also conform to the general division of the icosahedral symmetry group. (Please note that Point C does not rest on the great circle. The spherical sections of the icosahedral great-circles, when flattened, yield a Disdyakis Triacontahedron.)
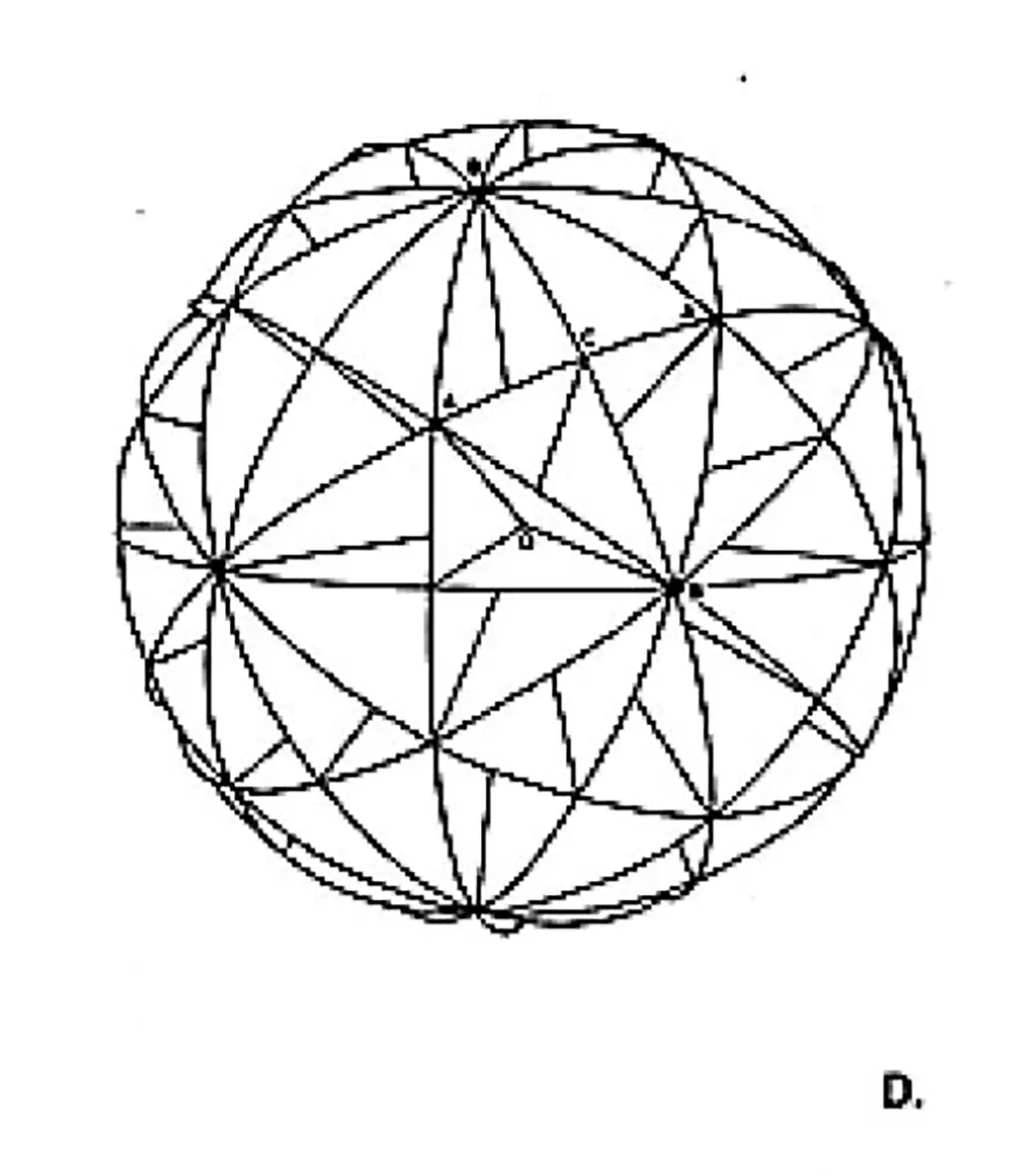
Fig. 986.502D Thirty Great-circles of the icosahedral symmetry group in relation to the division of the Rhombic Triacontahedron
Notably, the T Quanta module possesses exceptional properties concerning many other regular polyhedra, polyhedral stellations, space fillers, and other symmetric or (a-)periodic spatial arrangements. We will explore these in more detail later.
Upon unfolding, we observe the faces form a square surface. To clarify this, we rotate the smallest triangle. The edge length of this square also corresponds to the radius of the original Rhombic Triacontahedron.
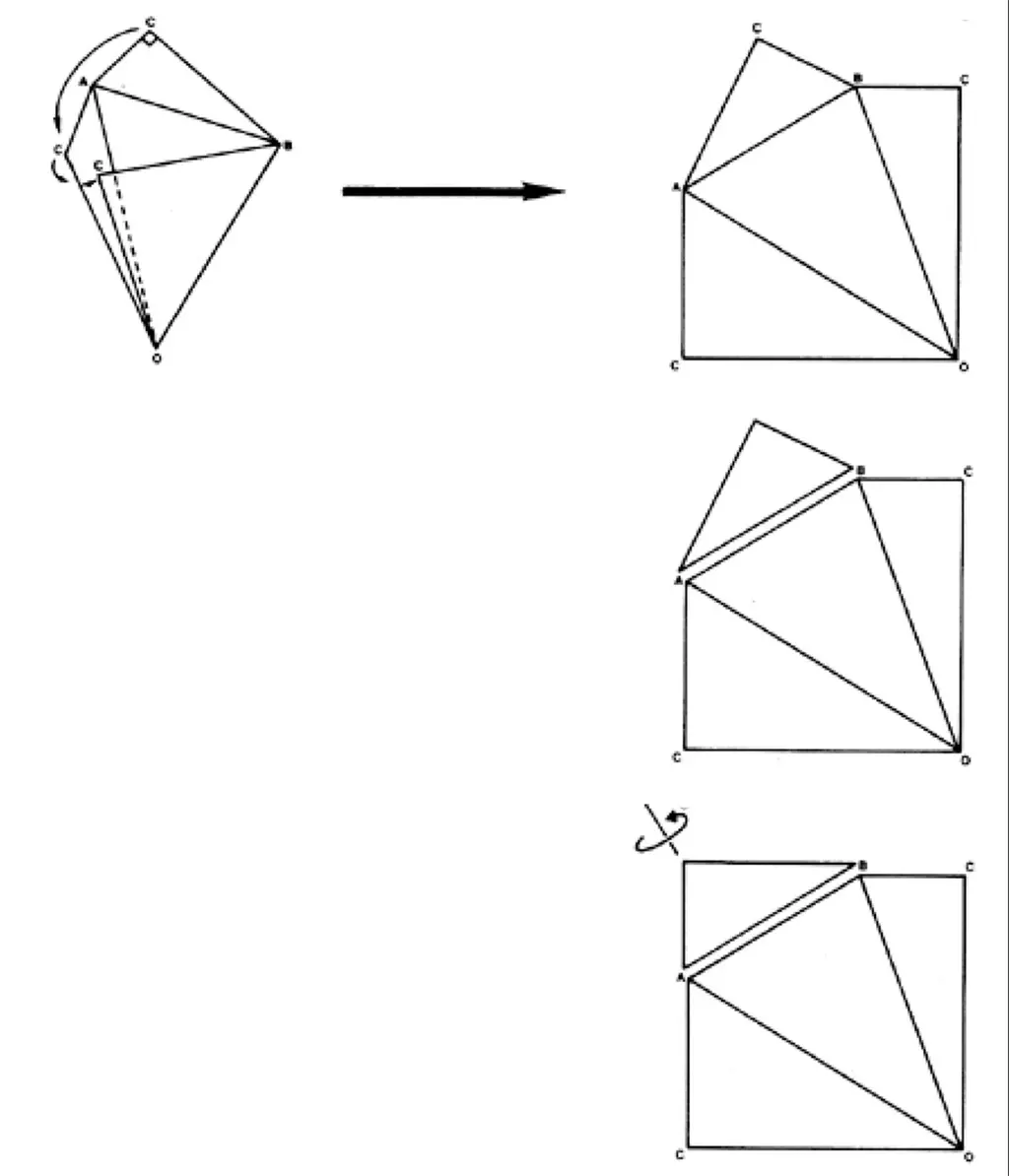
986.515 (Modified) – Unfolding of the T-Quanta Module
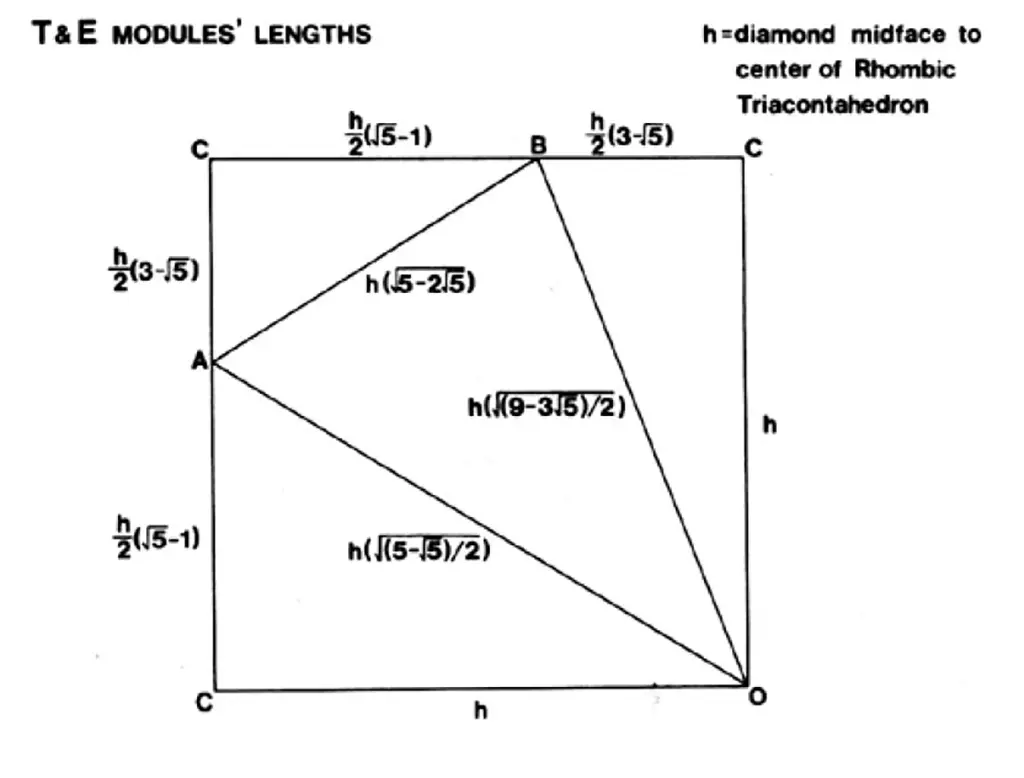
986.411A – Edge Lengths of the T Quanta Module in a plane
When we dissect the T Quanta module, it reveals a fundamental association with the Golden Ratio ( φ ). This number appears in various relations of edges, angles, areas, and volumes.
Given that this exploration ultimately transitions into a fractal (research) process, leading to the ‘Answer to the Ultimate Question of Life, the Universe, and Everything’, we shall leave it unexplored for now.
All illustrations are taken from Synergetics (1997), by R. Buckminster Fuller, but may be used in a different context to serve the authors simplified explanation.