Polyhedral Kaleidosphere I

In a small series of three posts I will describe the development of the Kaleidosphere – A sphere made out of Kaleidoscopes.

concept

All regular Polyhedrons are based on symmetry. There are the three symmetry groups which most of the follow:

• Tetrahedral
• Octahedral
• Icosahedral
• (Every rule has it´s exceptions there a few, not to follow any of this, but rotational symmetry. – I promised to write about this before. Still a promise.)

They look like this:

Tetrahedral – Octahedral – Icosahedral

Orange great circles show the symmetry group. Think of it as a plane going through each of the circles slicing the sphere into multiple parts.  If your polyhedron follows one of these groups, you can cut it with all of these planes and extract an “essence” of that shape. Without going into detail, this can be nailed down to the fact, that you can represent an entire sphere (or a inscribed polyhedron) by this essence and a set of mirrors, as long as you cut it out in the shape of these spherical triangles:

Animation showing how spheres can be sub-divided. This is the base of (almost) all regular polyhedral shapes.

So here is an example of the “essence” of that shape, which would be enough to represent this.

3d-Print which create a polyhedral shape, if dropped into a mirrored prism.

exploration

You may have seen an animation earlier which also rolls out these fractions on a plane. So if we can only take a part to represent the whole sphere, we can also take many parts, arrange them spherical and represent many polyhedrons at the same time.  Just imagine a bunch Kaleidoscopes glued together. Each angle you view the sphere you can discover a different shape inside.

Sketch of the physical model.

The physical model.

 Now that we know, we can insert a a mirror on any of these locations we can also work the other way around and remove mirrors from this sphere in order to merge the kaleidoscopes in to other shapes but the symmetry specific spherical triangle. Here is a little animation of showing how you can merge multiple triangles to bigger compounds. As you only remove a small part of the mirrors and replace it by the real thing it still works perfectly.

While this animation shows the spherical section in the joined surfaces.

As you see, with this method there is also a quite limited amount of shapes. This shall be extended to random merging later. Now let´s take these spherical sections and replace them by polyhedrons.

Some static examples of these merged sections:

Rhombic cut-outs on an icosahedral symmetry.

 

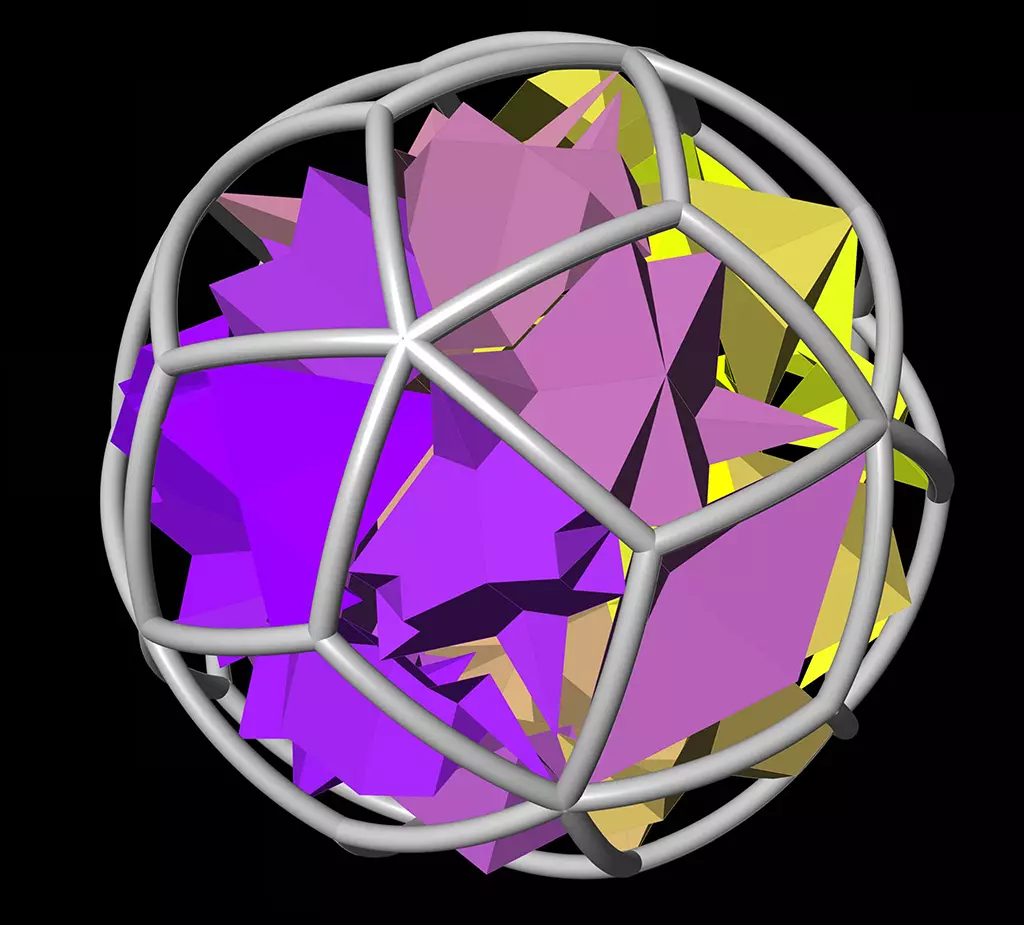
Merged sections (triacontahedral)

Pentagonal cut-outs on an icosahedral symmetry, divided with surface in the place of the mirrors.

Dodecahedral sections

Kite-shaped cut-outs on an icosahedral geometry. We can now also use any polyhedron shape following the outside to cut the mirrors instead of using the initial sphere.

Symmetric Kites

This is part I of III in the development of the concept of the Kaleidosphere. To be continued in part II.

 

links
https://en.wikipedia.org/wiki/Point_groups_in_three_dimensions 
https://en.wikipedia.org/wiki/Polyhedral_group 
http://mathworld.wolfram.com/SnubCube.html 
http://mathworld.wolfram.com/PentagonalIcositetrahedron.html