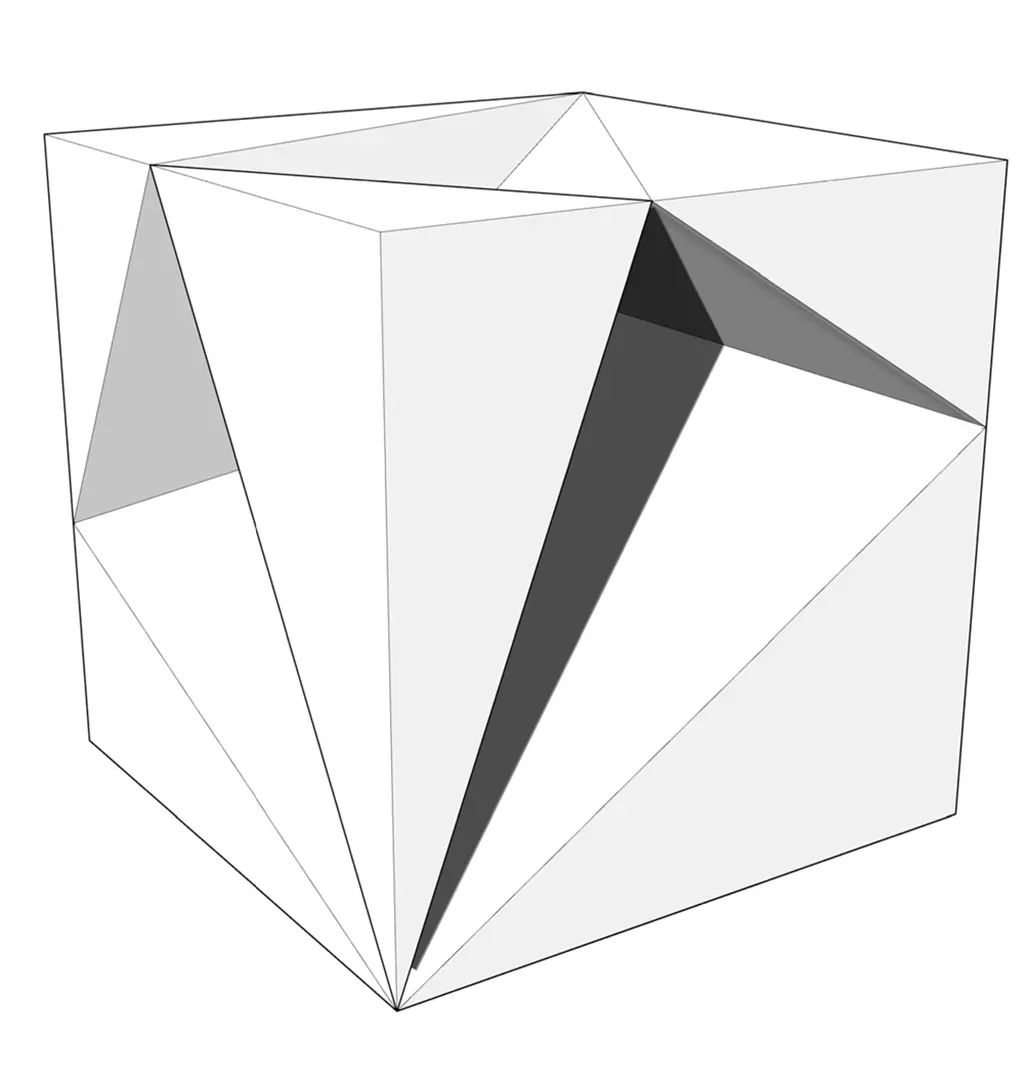
SuperCube – the missing link between four-fold and five-fold symmetry
SuperCube: A Marvel of Geometry
Renowned for his unique approaches, Einar Thorsteinn (1942 – 2015) developed the SuperCube. This innovative geometric arrangement was a direct result of his in-depth research around FANG, an acronym for Fivefold Symmetry – All Space Filling – Non-Periodic -Geometry.
FANG: The Genesis
Undeniably, Buckminster Fuller’s work served as a rich source of inspiration for Thorsteinn. As such, Thorsteinn devoted his efforts to deeply investigating polyhedral space fillers and spatial symmetries. In essence, FANG is an exploration of the distinct properties of Fuller’s T-Quanta Module. In his insightful essay ‘Fang Report I’ penned in 2004, Thorsteinn elaborated on the unique characteristics of the FANG-based fractal subdivisions and their integral relation to Five Fold Symmetry Space.

Thorsteinn´s model of a cubeFiveCompound strapped to a car. (Image: Studio Olafur Eliasson)
The Formation of SuperCube
Creating the SuperCube from the T-Quanta Module involves specific methodologies. Thorsteinn often initiated his explorations with simple two-dimensional drawings. It is presumed that he used a similar approach while conceptualizing the SuperCube.
T-Quanta modules and their unfolded, mirrored version.
Interestingly, the faces of the non-regular tetrahedron T-Quanta Module can be rearranged into a square. Once we consider this square as a face of a cube, six T-Quanta modules can be systematically arranged. In this arrangement, each module connects with three others at their vertices. Subsequently, subtracting these initial volumes from the cube leads to a fascinating transformation. Each corner of the cube morphs into a positive, while each of the former faces turns into a negative of the initial module. However, for this to occur, it is necessary for the square’s corner, which connects to the longer edges of the triangle, to meet thrice in one corner of the cube. Additionally, the cube’s opposing corners present as mirrored versions of each other.
Exploring Other Approaches
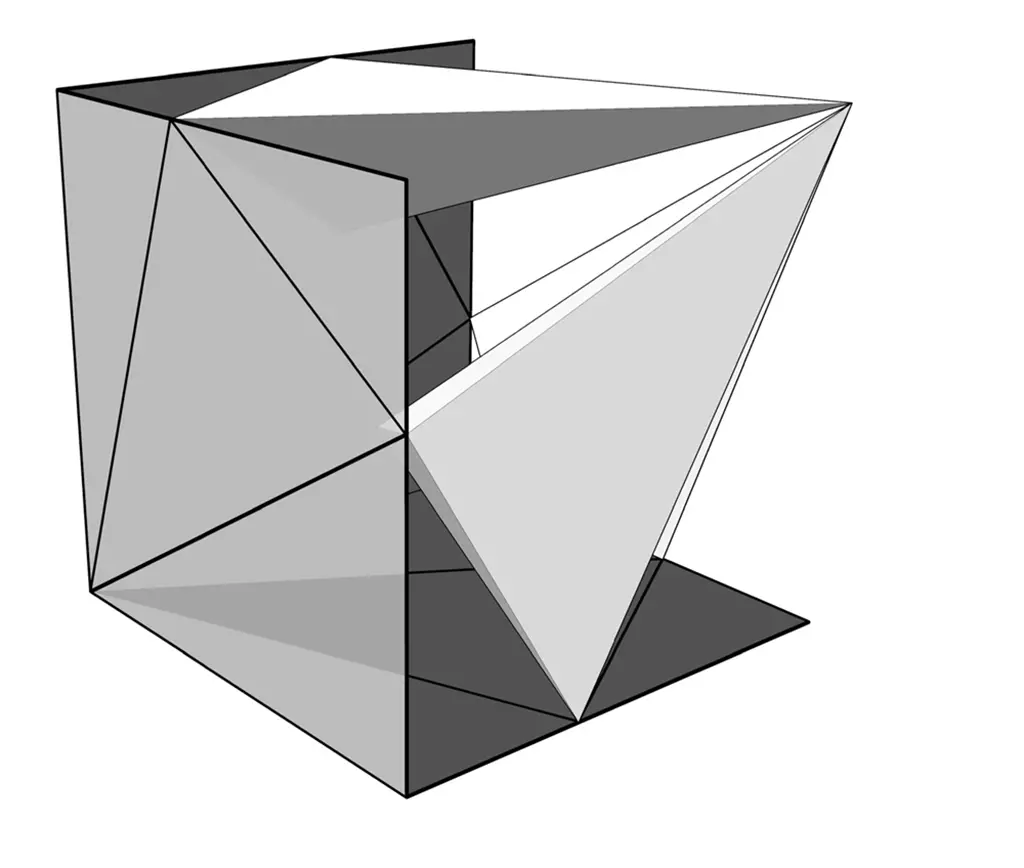
Yet another approach involves the use of a cube as the starting point. This cube, rotated around its diagonal axis, continues to turn until its edges divide each other by the golden ratio. Contrary to first impressions, this rotating angle isn’t 45° but is slightly lesser.
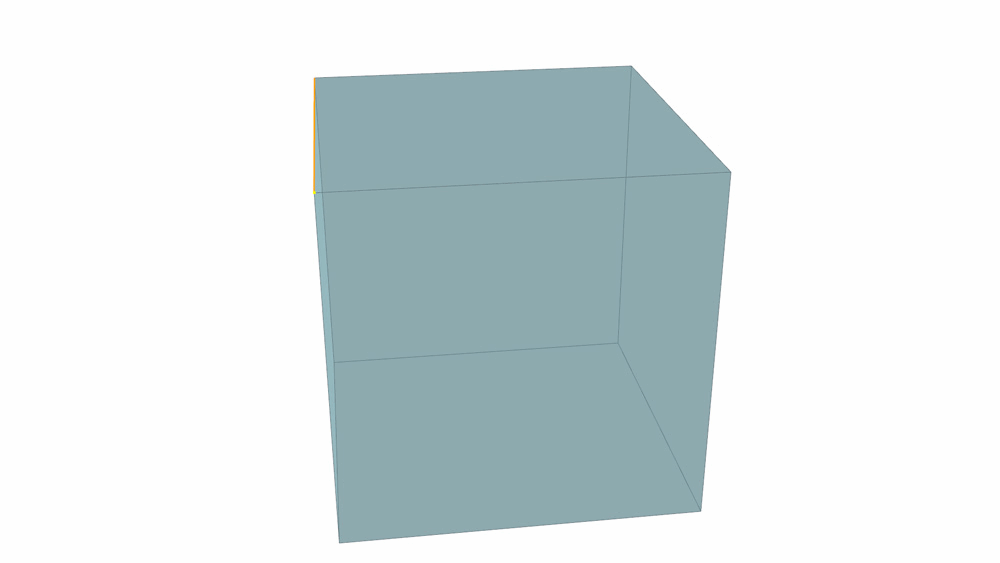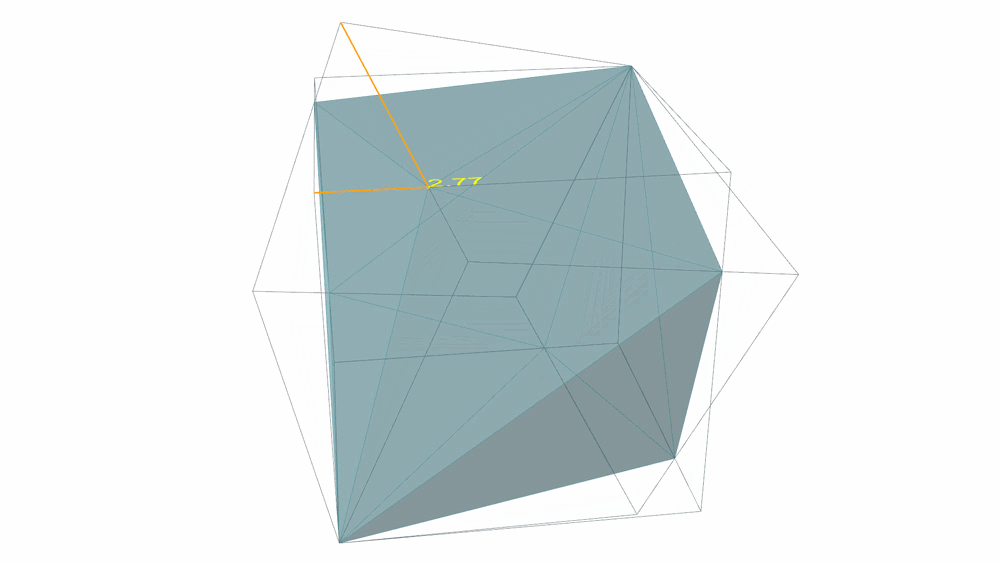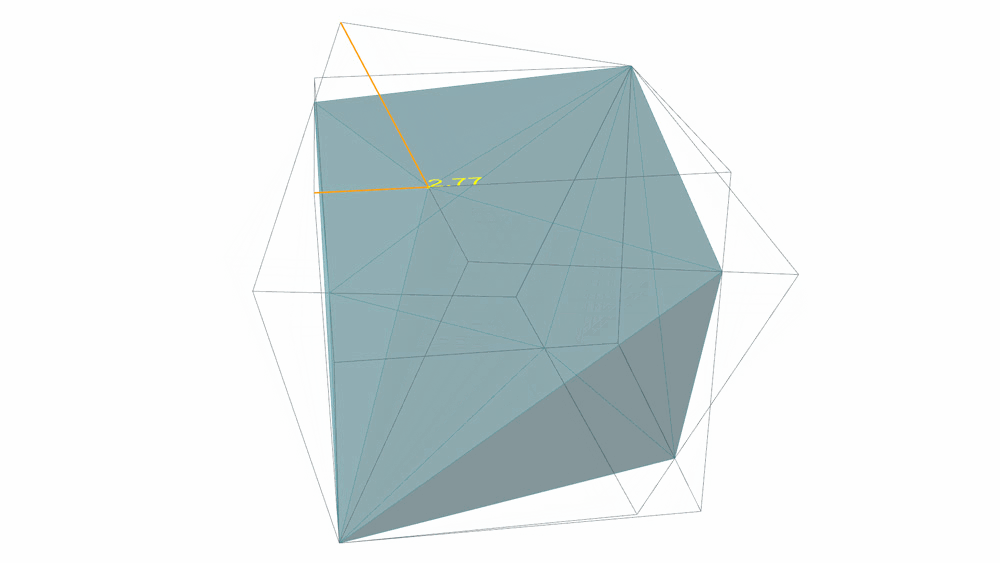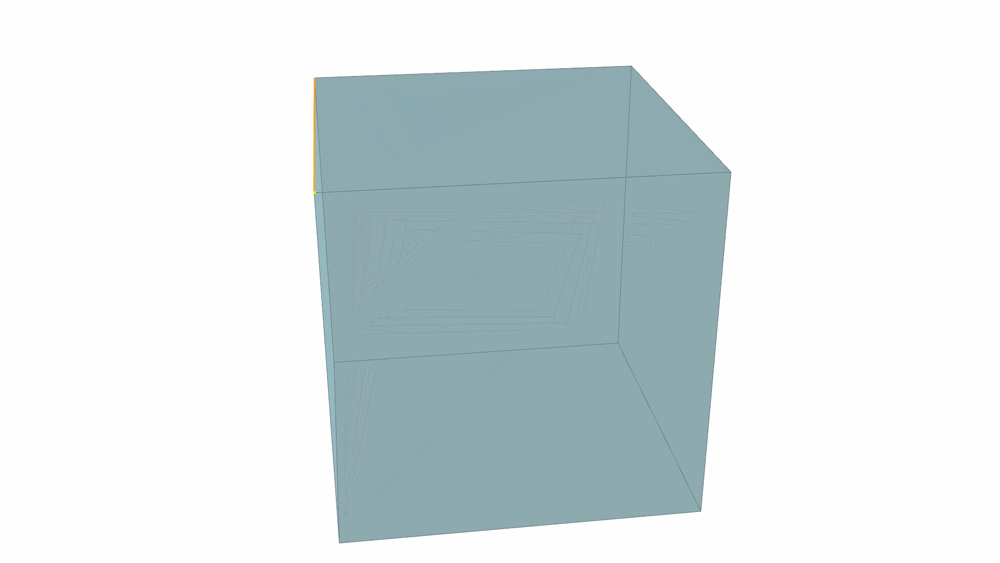
Rotating a Cube around its diagonal axis.
Such a transformation effectively subdivides both the initial and the rotated cubes into a series of T-Quanta modules. Employing this approach requires subtracting the initial volume from the rotated one, then mirroring the leftover modules towards the inside, and subtracting them once again from the first cube. Furthermore, it’s important to note that there are numerous pathways to arrive at the same result. For instance, operating on any two volumes of a regular compound of five cubes will also lead to the SuperCube. Such an observation provides insight into the geometry’s inherent dependency on tetrahedral and icosahedral symmetry.
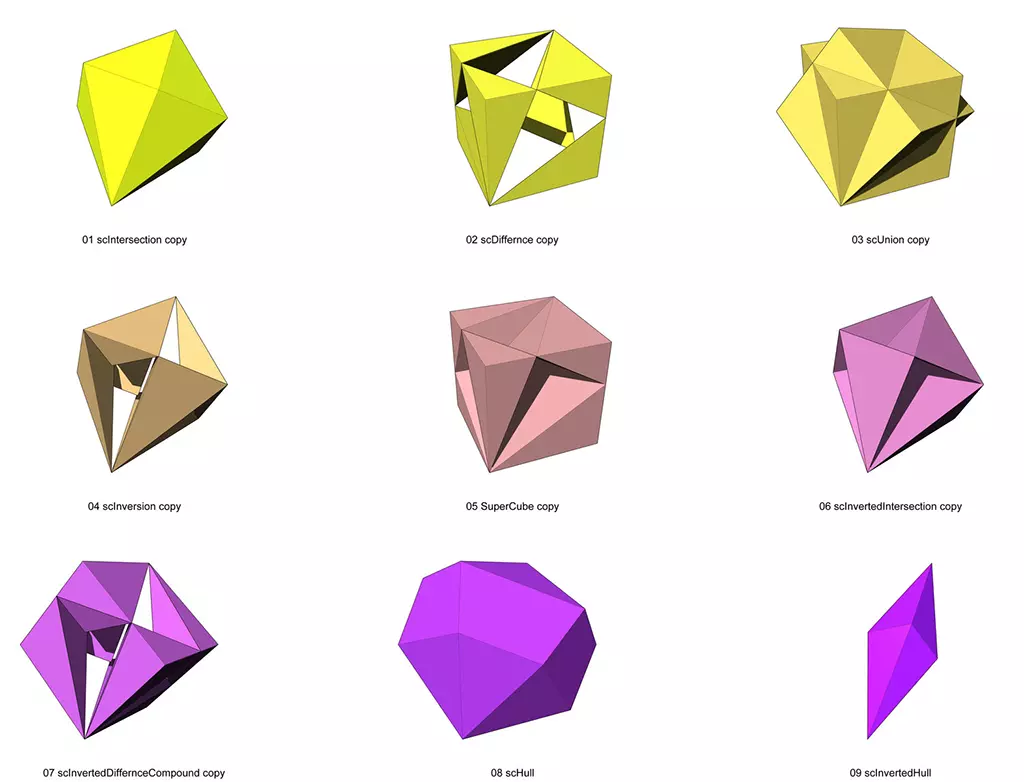
SuperCube variations
The Allure of the SuperCube
The SuperCube holds a captivating place in geometric studies due to its integration of different symmetry groups and their space-filling modules. It aptly illustrates the dual nature of the cube and the T-Quanta. While the cube is the simplest periodic space-filling element of fourfold symmetry space, the T-Quanta represents the aperiodic space filler of fivefold symmetry space. Consequently, the SuperCube opens up a plethora of configuration possibilities that are worth delving into further.
Further Reading Cube and compounds: http://www.georgehart.com/virtual-polyhedra/compound-cubes-info.html http://mathworld.wolfram.com/Cube5-Compound.html Einar Thorsteinn: http://crystaldesign.kingdomes.de/einar_stalke.html