Hopf Fibration

Decoding the Fourth Dimension: A Simplified Guide to Hopf Fibration

Welcome to an engaging journey that introduces you to the fascinating realm of the fourth dimension through the prism of Hopf Fibration. While this concept may seem complex, this guide simplifies it to make it understandable.

Unraveling the Hopf Fibration

In basic terms, Hopf Fibration is the stereographic projection of a 4-dimensional Sphere. However, the concept runs deeper. To explore it further, let’s begin with understanding stereographic projections of the 4th dimension.

Video by Niles Johnson

Visualization and the 4th Dimension

Typically, our understanding revolves around 3D objects, making the concept of higher dimensions challenging. However, specific methods can bring these higher dimensions down to a level we are familiar with, enhancing our understanding. In this case, we employ Hopf Fibration to transition the S3 (4-dimensional sphere) into the realm of 3D. Instead of attempting to project the entire surface of the S³ Sphere, which can be complicated, we focus on certain reference curves. This approach mirrors sketching a 3D surface on paper, where we draw curves following the topology to improve clarity.

Understanding Projections

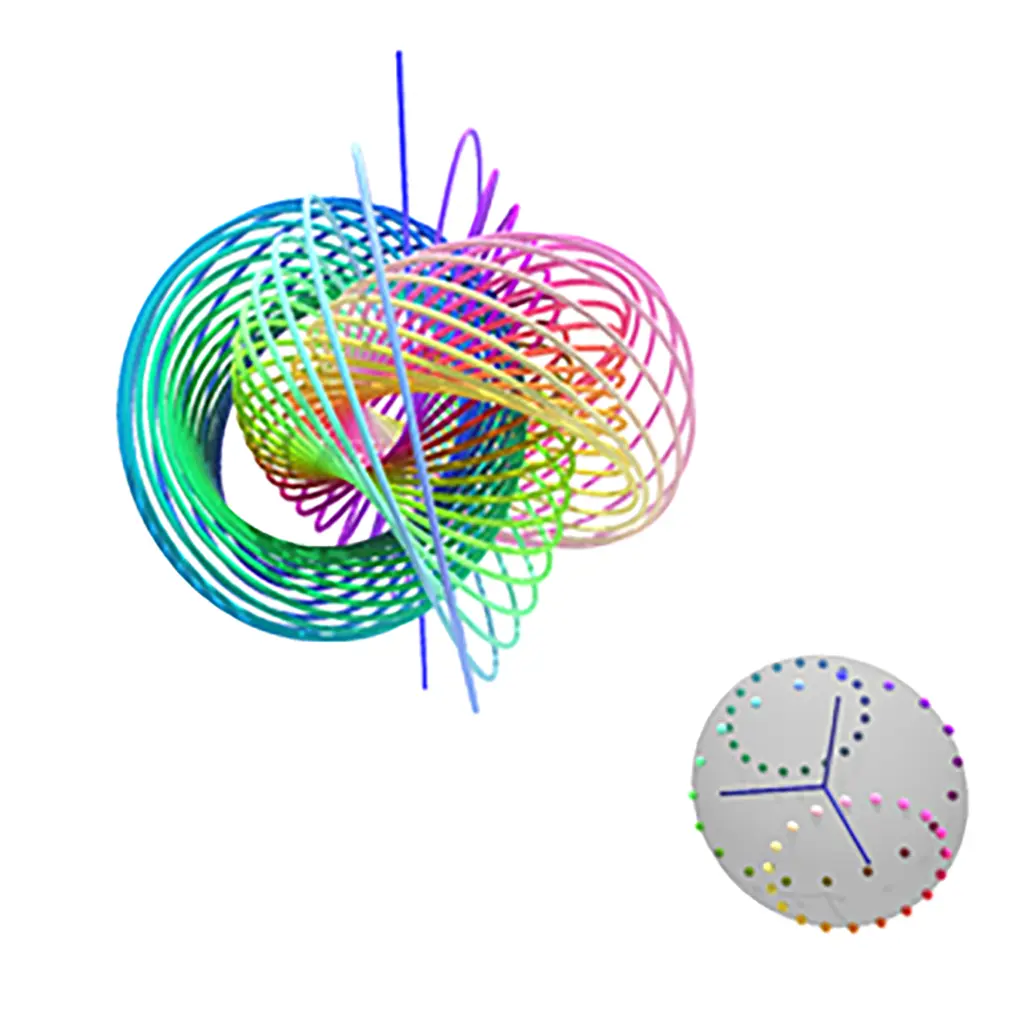
Just like we use latitudes or longitudes to understand spheres, we use a similar method here, but we call these ‘fibers.’ In essence, all these fibers are circles. However, their appearance changes based on how far they are from our ‘projection center’ or lamp. When they’re close, they appear as circles, but as they move away, they get distorted and may even become lines when very close to the projection origin. This is comparable to capturing an image of an elephant and printing it on paper. The image, while not the complete entity, aids in understanding the concept. Remember, “Ceci n’est pas une pipe.”

Hopf Fibration: Mapping and Projections

Now that we have the basics covered, let’s delve into the video above. It employs a unique method to project drawings onto a 3D map and then back onto the Hopf Fibration. Similar to our previous analogy of creating a flat map of the globe, we can map various elements from our globe to our flat map. Post this, we can then project these elements back onto our globe. We use the same technique with the Hopf Fibration. Every colored dot on the sphere in our initial image corresponds with a curve in space. Every dot on the map thus represents a circle. A circle on the map would be a torus on the projection, meaning a circle divided into dots on the map becomes a torus divided into circles in our projection. The closer the dots are to the lower pole on the map, the closer they come to the lamp, making their projection more precise. As a dot travels to the top of the sphere, it gets projected towards infinity, causing circles to bend. If a dot sits on the upper pole of the map, the projected circle extends from infinity to infinity, appearing as a line in our Hopf Fibration. Interestingly, all these fibers technically are Villarceau Circles. Our earlier discovery was just a subset of this concept. In simpler words, pick any two points on the spherical map, and they will always be interlocking circles in the projection.

Exploring Further

In the upcoming post, I will delve into the potential applications and implications of this intriguing method. Stay tuned!