In his work, Synergetics (1997), R. Buckminster Fuller introduces us to the world of innovative geometry with two unique tetrahedral shapes: the A-Quanta Module (913.00) and the B-Quanta Module (916.00). These distinct shapes serve as significant touchstones in our understanding of geometric design.
To construct the A-Quanta Module, a fascinating procedure comes into play. The process initiates with the equilateral tetrahedron, which is the first among the five platonic solids. This tetrahedron is then precisely divided into four separate sections. The outcome of this division is four identical, irregular pyramids that intersect at the very center of the original tetrahedron. Following this, we further partition this quartered tetrahedron by creating sections along the three perpendicular bisectors. The final product is a unique geometric shape that comprises a 1/24th (which is a 1/6th of a 1/4th) of the initial volume, now identified as the A-Quanta Module.
The A-Quanta Module stands out due to its characteristic divisions. This module can be split into six portions, each of which shares equal properties and proportions. Interestingly, these sections mirror each other in pairs of three, a concept that Fuller encapsulates as positive and negative (913.10). The A-Quanta Module has a set of distinctive properties, specifically its foldability, which fosters a compelling relationship with two-dimensional space. However, the full implications of this relationship extend beyond our current discussion and deserve further exploration.
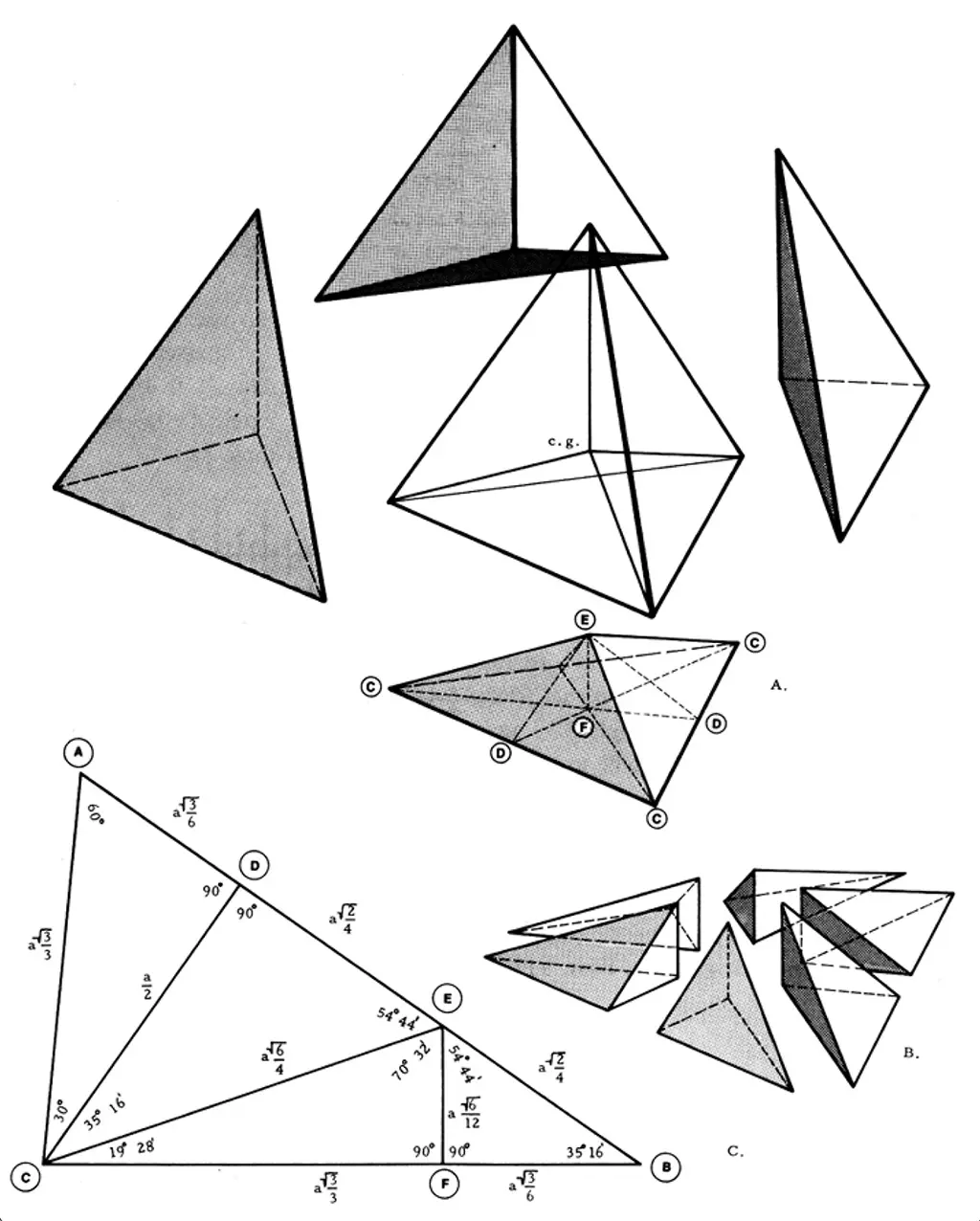
913.01 The A-Quanta Module from Synergetics
The B-Quanta Module is another marvel of Fuller’s geometric vision. The process for creating this module draws parallels with the A-Quanta Module. It involves starting with a regular octahedron, dividing it meticulously into eight equal parts, and further dividing it into six pyramids. Subtracting the A Module from this constructed shape results in the B-Quanta Module. This geometric entity possesses an equal volume to the A Module, making it a 24th of the original tetrahedron.
For a more comprehensive understanding of Fuller’s intriguing and complex geometric constructs, it would be worthwhile to explore the related description for the T-Quanta module. This detailed explanation will further enrich your insight into the wonderful realm of Fuller’s unique geometry.
All illustrations are taken from Synergetics (1997), by R. Buckminster Fuller, but may be used in a different context to serve the authors simplified explanation.