Bridges Conference (Virtual), 2020 – Phillip C. Reiner

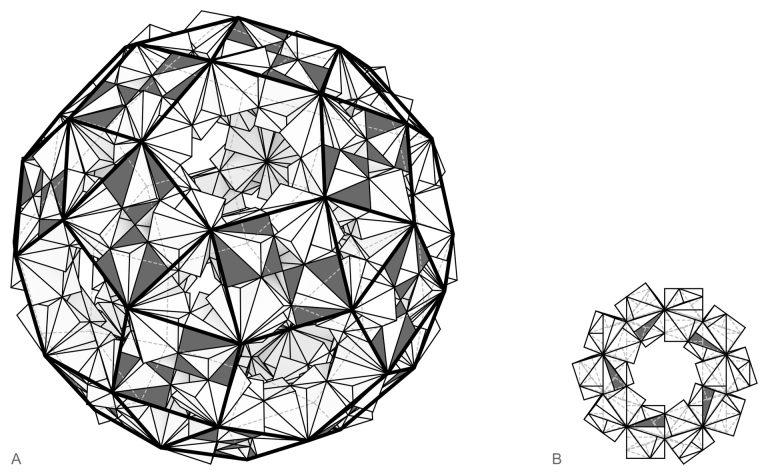
The Kaleidosphere is a prototype and an example of a broader study of models. A larger set of polyhedrons was grouped by their underlying (tetrahedral, octahedral or icosahedral) symmetry group and dissected with the corresponding planes. The resulting tetrahedral spherical arranged sections were merged with two of their neighbours into larger groups of four. In each of the resulting parts locations a different polyhedral section was kept. Mirroring surfaces in between those sections complete the only partially physical geometry. To maintain the correct image the polysurfaces had to be displaced from the overall centre. The mirrors were cut by a corresponding polyhedron of the underlying symmetry group.

Research:
Polyhedra are grouped by symmetry (tetrahedral, octahedral, icosahedral) and dissected with the matching symmetry planes. The resulting spherical sections are merged in groups of four; one polyhedral section is retained per group and mirror surfaces complete the form. The displacement of polysurfaces from the centre and the mirror cutting geometry were calculated so that the physical-mirror hybrid yields a single coherent image.